Problème et Modelisation
Problème
On cherche ici à animer un acteur, par exemple un véhicule, de telle sorte à ce que celui-ci se déplace pour rejoindre un point particulier dans l’espace.
Afin de réduire le problème nous nous restreindrons ici à deux dimensions, et nous placerons dans un cas où nous pouvons intéragir immédiatement avec la vitesse de nos objets. A tout moment la position et vitesse de l’ensemble des objets de la simulation peut-être connu.
Modélisation et pseudo-code
Nous utiliserons ici un véhicule pour représenter notre agent autonome. Dans les schémas suivants, celui-ci est noté “Vehicle”, et la cible “Target”. Un véhicule aura une vitesse maximale de déplacement, ainsi qu’une vitesse maximale de changement de direction.
Etapes 1-3: Calcul de la vitesse désirée
A chaque instant de la simulation nous connaissons la position de notre véhicule ainsi que de sa cible.
Nous pouvons donc connaitre la distance qui sépare notre véhicule de cette cible, ainsi que la direction dans laquelle il nous faudrait se déplacer (en ligne droite !) afin de la rejoindre.
En soustrayant la position du véhicule à celle de notre cible, l’on obtient un vecteur représentant le mouvement que devrait effectuer notre véhicule pour rejoindre sa cible [1]. Si l’on normalise ce vecteur (garder son sens et direction mais ramener sa norme [longueur] à 1), nous obtenons donc la direction à suivre [2]. Il nous reste à multiplier ce dernier vecteur normé par la vitesse maximale de notre véhicule afin d’obtenir la vitesse désirée [3].
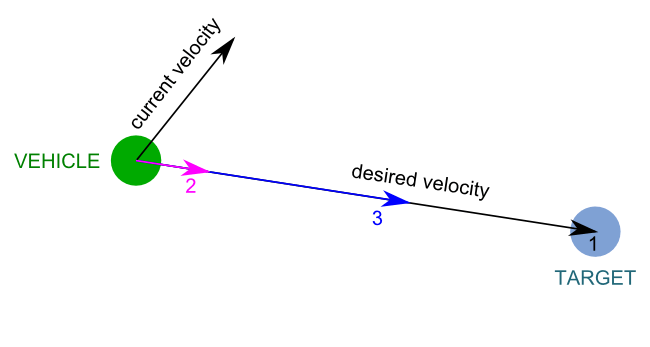
- Vector (desired velocity) = Position (target) – Position (vehicle)
- Normalize Vector (desired velocity)
- Scale Vector (desired velocity) to the maximum speed
Etapes 4-5: Calcul de la force de direction
En plus de connaitre les positions de nos objets, nous connaissons aussi leur vitesses. Notre véhicule lui-même a, à chaque instant, une vitesse courante mesurable (current velocity), avec sa propre direction et intensité.
Les changements d’orientation de notre véhicule sont modelisés par une force de changement de direction, qui nous permet de représenter le comportement de conduite. Notre véhicule possède une valeur maximale pour cette force de changement de direction, qu’il ne devra donc pas pouvoir dépasser.
Conceptuellement, cette force représente le changement de direction que l’on veut voir notre véhicule réaliser. Nous pouvons donc la calculer comme étant la différence entre la vitesse désirée et la vitesse actuelle [4], puis en limitant l’intensité de ce vecteur à la force maximale du véhicule [5].
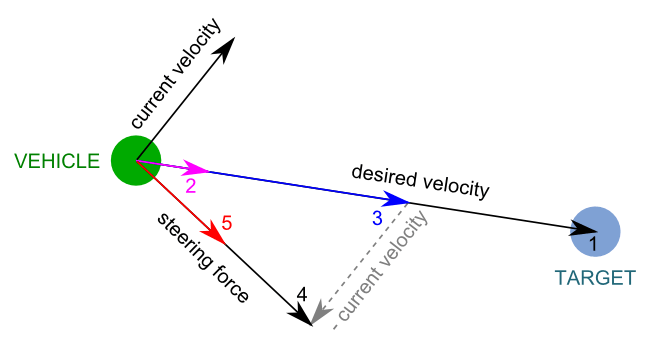
- Vector (steering force) = Vector (desired velocity) – Vector (current velocity)
- Limit the magnitude of Vector (steering force) to the maximum force
Etapes 6-7: Calcul de la nouvelle vitesse
Connaissant notre vitesse de déplacement actuelle ainsi que la “force” à appliquer à celle-ci pour s’orienter vers notre vitesse désirée, nous pouvons calculer la nouvelle vitesse instantanée.
Celle-ci est en effet la somme de notre vitesse actuelle ainsi que de la force de changement de direction [6], limitée par la vitesse maximale de notre véhicule [7].
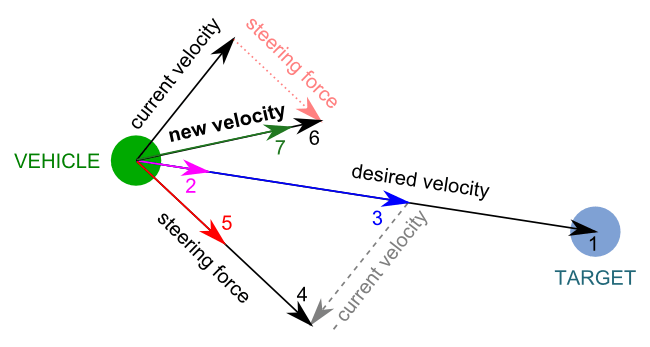
- Vector (new velocity) = Vector (current velocity) + Vector (steering force)
- Limit the magnitude of Vector (new velocity) to the maximum speed